Wie kann man durch eine einfach nachzuvollziehende Symbolik ein eingestelltes Gleichgewicht von einem System unterscheiden, das auf dem Weg zum Gleichgewicht ist? Wie könen Schüler/innen die Reaktion auf eine Störung sowie die veränderte Zusammensetzung eines Gleichgewichts nach der Störung anschaulich darstellen? Die Gleichgewichts-Schreibweise ist dazu wenig geeignet. Präzise Formulierungen tragen aber dazu bei, solche und ähnliche Sachverhalte besser zu verstehen. Es werden Sprech- und Darstellungsweisen zu diesen Fragen vorgeschlagen, die die Diskussion darüber in Gang bringen sollen.
1 Sprech- und Darstellungsweisen auf dem Prüfstand
Bei Betrachtungen zum chemischen Gleichgewicht und dessen Beeinflussungen durch Konzentrations-, Druck- oder Tempe- raturänderungen, wird in der Versprachlichung häufig nicht sauber unterschieden zwischen einer Argumentation über das Prinzip von LE CHATELIER einerseits (d. h. einer Störung durch einen äußeren Zwang und den darauf erfolgenden Reaktionen des Systems) und Aussagen zur Lage des chemischen Gleichgewichts über das Massenwirkungsgesetz und die Gleichgewichtskonstante K andererseits.
Dieselbe Problematik schlägt sich letztlich auch in der chemischen Symbolsprache nieder, wie im Folgenden verdeutlicht wird:
Die so genannte »Verschiebung« oder »Verlagerung« eines Gleichgewichts wird häufig durch einen dickeren oder längeren Pfeil des Gleichgewichtdoppelpfeils symbolisiert:
Beispiel 1:
»Durch Konzentrationssenkung des Esters (= Produkt) wird das Gleichgewicht nach rechts verschoben.«

Beispiel 2:
»Temperaturerniedrigung führt zur Verschiebung des Gleichgewichts in Richtung der exothermen Reaktion, also nach rechts.«

Die kaum zwischen dem Gleichgewichtszustand und dem Prozess der Einstellung eines chemischen Gleichgewichts unterscheidende Sprechweise von Chemikern schlägt sich auch in Äußerungen wie »im Gleichgewicht sind die Geschwindigkeiten von Hin- und Rückreaktion gleich groß« nieder.
2 Verwirrungspotenzial obiger Sprech- und Darstellungsweisen
Ein Stoffsystem im chemischen Gleichgewicht verhält sich völlig anders als eines, das sich (noch) nicht im Gleichgewicht befi ndet. Es ist daher sinnvoll, zwischen beiden Systemen zu unterscheiden.
»Verschiebung« oder »Verlagerung« eines Gleichgewichts wird häufi g mit der Vorstellung verbunden, dass die Konzentrationen der Teilchen auf einer Seite des Gleichgewichtssymbols alle zuund die der Teilchen auf der anderen Seite alle abnehmen. Dies trifft aber ausschließlich auf Temperaturänderungen zu.
In diesem Zusammenhang bergen daher folgende vier Aspekte Verwirrungspotenzial für Lernende:
A) Gleiche Symbolik für unterschiedliche Sachverhalte
- Der Gleichgewichtspfeil mit einem größer gezeichneten Pfeil gibt einerseits die ungefähre Lage eines Gleichgewichts an (Gleichgewichtskonstante K >> 1), andererseits besagt er »das System ist (noch) nicht im Gleichgewicht, die Reaktion nach rechts überwiegt.«
- Der Unterschied zwischen chemischer Reaktion (einem Prozess) und chemischem Gleichgewicht (einem Zustand) wird durch Verwendung derselben Pfeile nicht deutlich. So kommt es zu Fehldeutungen über die Bedeutung der stöchiometrischen Faktoren der Reaktionsgleichung. Sie werden oft als Angaben über die Zusammensetzung des Gleichgewichtgemischs missverstanden.
B) »Verschiebung eines Gleichgewichts« bedeutet einerseits: Es stellen sich neue Konzentrationen aller beteiligten Teilchen ein, die Gleichgewichtkonstante ist wieder dieselbe wie vor der Beeinfl ussung. Dies trifft für Druck- und Konzentrationsänderungen zu. Andererseits kann damit aber auch gemeint sein: Es stellt sich ein neues Gleichgewicht mit einer anderen Gleichgewichtkonstanten ein. Dies ist ausschließlich bei Temperaturänderungen der Fall.
C) Ohne Veranschaulichungsmöglichkeit ist die tatsächliche veränderte Zusammensetzung eines Gleichgewichts infolge eines Einflusses von außen schwer zu beschreiben und bleibt deshalb oft unklar.
D) Das chemische Gleichgewicht wird immer wieder dadurch als dynamisches Gleichgewicht charakterisiert, dass man formuliert: Die Reaktionsgeschwindigkeiten von Hin- und Rückreaktion ändern sich nicht mehr, sie sind gleich groß. Die Reaktionsgeschwindigkeit ist aber eine zur Beschreibung des Gleichgewichtzustands ungeeignete Größe. Da sie defi niert ist als Konzentrationsänderung pro Zeiteinheit, sich die Konzentrationen der an einem Gleichgewicht beteiligten Stoffe aber mit Erreichen des Gleichgewichtzustandes nicht mehr ändern, sind die Geschwindigkeiten von Hin- und Rückreaktion zwar sehr wohl gleich groß, aber immer unabhängig vom betrachteten Gleichgewicht gleich Null. Was eigentlich zum Ausdruck gebracht werden soll, nämlich, dass pro Zeiteinheit gleich viele Hin- wie Rückreaktionen stattfi nden, kann daher über die Reaktionsgeschwindigkeiten nicht verdeutlicht werden.
3 Vorschläge zur Minimierung von Verwirrung und Verständnisschwierigkeiten
Zu A) Für Systeme, die tatsächlich im chemischen Gleichgewicht sind, wird ausschließlich das Gleichgewichtsymbol verwendet (»Harpunen«, z. B. Schrifttyp Lucida Sans Unicode, Zeichencode 21CC):

Die extreme Lage eines Gleichgewichts kann durch Vergrößerung der oberen oder unteren Harpune ausgedrückt werden:
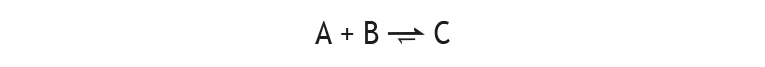
Will man hingegen ausdrücken, dass das System nicht im Gleichgewicht ist und die Reaktion nach rechts überwiegt, wird der normale Reaktionspfeil verwendet. Dabei kann die ebenfalls noch ablaufende Reaktion in die andere Richtung entweder vereinfachend weggelassen oder durch einen kleinen Reaktionspfeil angedeutet werden (hier eingeklammert):
Reaktion nach rechts:

Zu B) Anstelle »Verlagerung« oder »Verschiebung nach rechts«:
Bei Konzentrations- oder Druckänderungen formuliert man: Reaktion nach rechts bzw. links, bis zur Wiedereinstellung des Gleichgewichts (mit demselben Wert für K). Bei Temperaturänderungen hingegen: Reaktion nach rechts bzw. links bis zur Neueinstellung des Gleichgewichts (mit verändertem Wert für K).
Zu C) Veränderungen der Zusammensetzung eines Gleichgewichtgemischs durch eine Störung kann man durch halbquantitative Kreisdiagramme darstellen, in denen mithilfe von Pfeilen die Tendenz der Veränderung veranschaulicht wird: Die ausgefüllten Kreisausschnitte entsprechen den jeweiligen Konzentrationen.
Beispiel 1: Störung eines Estergleichgewichts durch Entzug eines Teils des Esters:
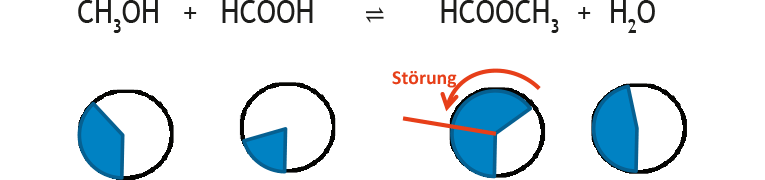
GG-Konstante: K
Nach der Störung ist das System nicht mehr im Gleichgewicht, es wird also nicht mehr mit dem Gleichgewichtsymbol sondern mit normalen Reaktionspfeilen gearbeitet. Die momentan nach der Störung vorliegenden Konzentrationen sind keine Gleichgewichtkonzentrationen und werden daher wie die Störung rot markiert.
Reaktion auf Störung:
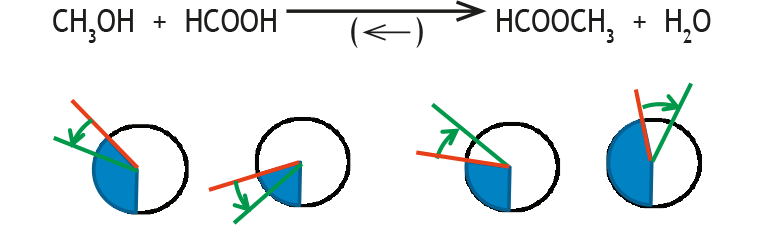
Diese Darstellung ist hilfreich, um die Rolle der stöchiometrischen Faktoren zu verdeutlichen: Während die Zusammensetzung des Gleichgewichts (blaue Kreisausschnitte) oder die Störung (roter Pfeil) durch sie nicht beschrieben wird, sind sie entscheidend bei der Reaktion auf die Störung (grüne Pfeile). Im obigen Beispiel ist darauf zu achten, dass diese alle gleich lang sind, da die stöchiometrischen Faktoren alle gleich sind. Ein stöchiometrischer Faktor von 2 müsste durch einen doppelt so langen grünen Pfeil veranschaulicht werden.
Wieder eingestelltes Gleichgewicht (K unverändert):
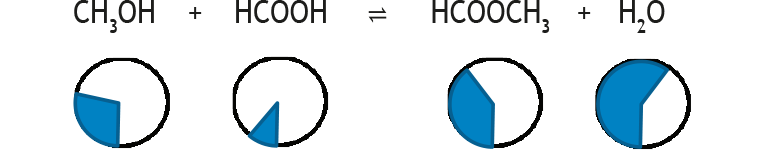
GG-Konstante: K
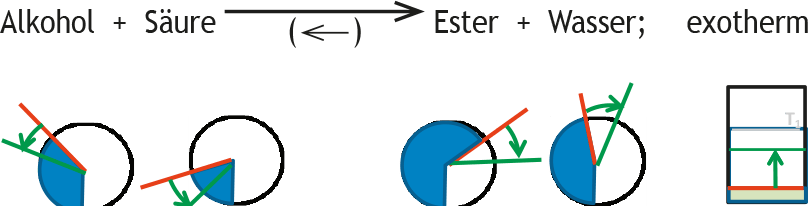
Beispiel 2: Störung durch Temperaturerniedrigung bei einem Estergleichgewicht, wobei die Bildung von Ester und Wasser exotherm ist. Die erniedrigte Temperatur wird von außen nicht konstant gehalten. Die Störung wird in einem symbolisierten Thermometer mithilfe eines roten Pfeils in der Tendenz veranschaulicht.

GG-Konstante: K1
Reaktion auf Störung:
Wie im ersten Beispiel gilt: Nach der Störung ist das System nicht mehr im Gleichgewicht, es wird also nicht mehr mit dem Gleichgewichtsymbol sondern mit normalen Reaktionspfeilen gearbeitet. Die momentan nach der Störung vorliegenden Konzentrationen sind keine Gleichgewichtkonzentrationen mehr und werden daher wie die Störung rot markiert.
Die Reaktion auf diese Störung führt zum verstärkten Ablauf der exothermen Reaktion, wodurch die Temperatur des Systems wieder ansteigt, allerdings nicht bis zum Ausgangswert. Dieser Schritt wird mit grünen Pfeilen angegeben.
Neu eingestelltes Gleichgewicht (K verändert):
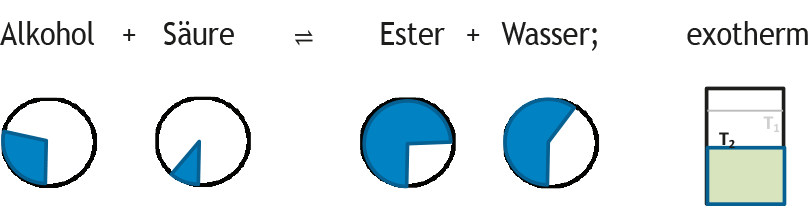
GG-Konstante: K2 > K1
Der einfachere Fall, dass die Temperatur nach der Störung konstant gehalten wird, lässt sich problemlos in analoger Weise darstellen.
Zu D) Im Gleichgewichtzustand sollte statt der Reaktionsgeschwindigkeit die Reaktionsrate zur Argumentation herangezogen werden. Sie bezieht sich nicht auf Konzentrationsänderungen, sondern auf die Zahl erfolgreicher Zusammenstöße der Reaktionspartner. Dadurch kann die Dynamik des Gleichgewichtes in der gewünschten Weise fachlich korrekt beschrieben werden.
4 Abwägung
Die zunächst zielführend erscheinende strenge Unterscheidung zwischen Wiedereinstellung und Neueinstellung kann später im »Chemiker-Jargon« wieder zu »Verschiebung« nivelliert werden. Wenn dann tragfähige Vorstellungen entwickelt wurden, erscheint diese Differenzierung eher als unerheblich. Gleiches gilt für die klare Unterscheidung von Reaktionsgeschwindigkeit und -rate.
Die Darstellung mithilfe der Kreisdiagramme ist sicher aufwändig, aber kann den Lernenden durch ihre klare Visualisierung der ablaufenden Veränderungen helfen, die Vorgänge bei Gleichgewichtbeeinfl ussungen von außen zu verstehen. Ob die Unterscheidung zwischen Gleichgewichts- und Reaktionspfeil didaktisch sinnvoll ist oder nur eine weitere Komplikation darstellt, bleibt abzuwarten.
5 Impulse zum Weiterdenken
- Wie könnte man mithilfe einer solchen Darstellung den Lernenden plausibel machen, dass sich bei Druckänderungen die Gleichgewichtkonstante niemals ändert?
- Könnte man bei einer Gleichgewichtbeeinflussung durch Druckvariation überhaupt die Änderungen in den Konzentrationen, Stoffmengen, Partialdrucken mit einer solchen Darstellung transparent machen (denken Sie insbesondere daran, dass eine Druckänderung nicht nur durch Volumen- oder Stoffmengenänderung erreicht werden kann, sondern auch durch Zugabe eines Inertgases)? Wäre dies sinnvoll?
- Auch die Einstellung eines Gleichgewichtes geht von einem System aus, das sich noch nicht im GG befindet. Lassen sich die vorgeschlagenen Sprech- und Darstellungsweisen auf diesen Fall übertragen?
Nehmen Sie Stellung zu diesem Vorschlag, berichten Sie von Reaktionen Ihrer Lernenden, beteiligen Sie sich am didaktischen Prüfstand: Schreiben Sie uns Ihre Kommentare und Anregungen.
Zusammengestellt auf Grundlage der Ergebnisse einer Arbeitsgruppe »Didaktischer Prüfstand« bei der MNU-Chemie-Bundesfachleitertagung 2016 von MATTHIAS KREMER und CARSTEN TITTEL.
MATTHIAS KREMER, , Staatliches Seminar für Didaktik und Lehrerbildung (Gymnasien), Königstr. 31,78628 Rottweil, ist Bereichsleiter Naturwissenschaften und Fachleiter für Chemie.
CARSTEN TITTEL, , Staatliches Seminar für Didaktik und Lehrerbildung (Gymnasien), Mathildenstr. 32, 72072 Tübingen, ist Fachleiter für Chemie.
